6-1. 매개변수 갱신 (Optimizer and Optimization problem)
매개변수 갱신이란?
신경망 학습의 목적은 손실 함수의 값을 가능한 한 낮추는 매개변수를 찾는 것이다. 이는 곧 매개변수 즉 parameter 의 Loss function 에 대한 최적값을 찾는 문제가 된다.
최적의 매개변수 값을 찾는 단서로 매개변수의 기울기(미분)을 이용하였다.
1. Gradient Descent
경사하강법(Gradient Descent)의 경우도 마찬가지이다. 단순하게 어떤 Error 에 대한 함수인 Loss function or Cost function 이라고 불리는 것을 정의하고 그것을 최소로 만들어 줄 수 있는 매개변수를 찾기 위하여 weight 와 bias 를 갱신하여주는 과정을 사용하였다.
여기서 간단하게 직관적으로만 생각하고 넘어갈 생각이지만, Gradient Descent 는 대체로 Batch Gradient Descent 와 Stochastic Gradient Descent 라는 두 갈레로 나뉘게 된다. [물론 두 가지 방법의 짬뽕으로 mini-batch gradient descent 가 있다.]
(1) Batch Gradient Descent
Batch 란 어떤 묶음을 말하고 있는 것인데, 딥러닝이나 머신러닝 분야에서는 이러한 batch 를 데이터 다발이라고 생각하면 간편하다. 1천만개의 데이터이던 100억이 넘는 데이터이던 한번에 하나의 묶음으로 생각하고 반복적으로 매개변수를 갱신하자는 것이다.
이것의 문제점은 무엇일까? 간편하게 생각해보면 gradient descent 의 연산에서 떠올려보면 가령 1억개가 넘는 데이터셋이라면 1억개에 달하는 데이터에 대한 가중치의 갱신을 위해 매번 iteration 마다 1억개에 대한 각각의 가중치를 기억하고 넘어가야하는 문제가 생긴다. 이것이 과연 효율적일까? 단언컨데 그렇지 않다.
(2) Stochastic Gradient Descent
위의 이러한 문제를 해소하려는 노력으로 concept 을 잡고 생각한 결과가 1억개의 데이터에서 일부만 가지고와서 처리해보면 어떻게 될까? 라는 것이다. 가령 1억개의 데이터 중 1만개를 가지고와서 처리한다고 생각하면 두 방법의 동일한 연산시간에 대하여 반복학습을 할 기회를 더욱 많이 얻게 되는 것이다. 하지만 모든 일이 그렇듯 특정 부분에서 생기는 이득이 있다면 예상하지 못한 손해도 발생할 수 있는 것 처럼 BGD 의 경우 전체 데이터를 꼼꼼하게 살펴보았기 때문에 물론 많은 시간을 투자해야겠지만 global optima 로 차츰 따라가는 것이다. 하지만 SGD 의 경우 그 근방을 뱅뱅 도는 경우가 존재한다.
하나의 단점을 더 언급하고자 하는데 그것은 비방등성 함수(anisotropy function)에 대한 문제이다.
** anisotropy function : 방향에 따라 성질, 즉 이 부분에서 언급하고 싶은 것은 기울기가 달라지는 함수이다.**
예를 한번 들어보면 f(x, y) = 1/20 * x^2 + y^2 라고 가정하겠다.


각 point 에서 gradient 가 향하는 방향이 어떤가? 0에서 정확히 수렴을 고집하는 것이 아니다. 이것이 가장 중요한 점이다. 이러한 경우 global minimum 이 되는 parameter 를 SGD 의 경우 잘 찾지 못한다.
mini-batch gradient descent : 앞선 Stochastic gradient descent 와 거의 용어적으로나 쓰임으로 혼용되고 있지만, 잠깐 살펴보면 언급하지 않았지만 stochastic 이란 단어가 붙는 이유는 전체 데이터에서 샘플 추출을 할 때, 확률적으로 보통의 경우 random 하게 초이스를 한다. 그렇기 때문에 이렇게 이름이 붙어있는 것이다. 아무튼 이러한 확률적으로 추출된 작은 batch --> mini-batch 를 여러게 뽑게된다. 예를들어 k개의 mini-batch 가 있다면 k를 연산을 각자 수행하여 이때 발생하는 gradient 의 평균을 구하여 사용하고자 한다는 말이된다. k개를 왜 나누어서 여러번 학습을 하는가? 간단하다. 전체 데이터셋은 너무 무겁지만 나누어진 데이터 하나하나는 조금 더 학습 시간이 짧다 그리고 가장 중요한 점은 GPU 에서 병렬 연산이 가능하다는 것이다. 이것이 mini-batch gradient descent 가 앞선 두가지 방법보다 보편적으로 많이 사용하는 이유가 된다.

이후의 optimizer 에 다룰 대한 발전은
1. Gradient 를 수정한 : Momentum, Nag(이 포스팅에서는 다루지 않는다)
2. Learning rate 를 수정한 : AdaGrad, RMSProp, Adadelta(x)
1 & 2 : Adam, NAdam(x)
앞으로 이어질 optimizer 에 대하여는 정확하게 핵심만 잡고 넘어갈 생각이다.
아래의 내용의 출처 : https://www.sravikiran.com/GSOC18/page2/
이 곳에서 방정식의 figure 를 사용하였다.
GSoC'18 @ CERN · Professional Blog
20 Jul 2018 In this blog post, I’ll be explaining the implementation of Adagrad and Adadelta optimizers. Adagrad: AdaGrad is an optimization method that allows different step sizes for different features. It increases the influence of rare but informativ
www.sravikiran.com
2. Momentum
Momentum 이라는 단어의 특징부터 바라보자! 뜻이 운동량이라는 단어이다.

각 parameter 를 해체하자!
v 는 물리학적 특징 답게 속도(velocity)로 해석할 수 있다. gamma 는 마찰계수 정도로 생각해보는 것이다!
그렇다면 v 가 갱신되는 것은 loss 가 수렴해야할 방향을 향하여 적절한 마찰계수를 받으며 감속하며 경사를 하강하고 있는 것이다.
그 후 theta 의 경우 이전의 속도에 학습률을 곱하여 갱신하는 것으로 마무리한다.
3. AdaGrad
신경망 학습에서는 학습률 (learning rate) 값이 굉장히 중요하다. 이 값이 너무 작은 경우 학습 시간이 너무 길어지고, 반대로 너무 크면 발산하여 학습이 제대로 이뤄지지 않는다.
**발산하다? : 아래와 같이 너무 큰 경우 한 값으로 집중하여 경사 하강을 하지 않고 이리저리 튀는 답답한 상황이 된다.

이 학습률을 정하는 효과적 기술로 학습률 감소(learning rate decay) 가 있다. 이것은 학습을 진행하면서 학습률을 점차 줄여가는 방법이다. 처음에는 큰 값으로 성큼성큼 학습을 하다가 조금씩 작게 학습한다는 것이다.
AdaGrad 는 개별적으로 매개변수에 적응적(adaptive)으로 학습률을 조정하는 학습을 진행한다.

간단하게 컨셉을 다시 한번 집고 넘어가자면 각 매개변수들이 update 할 때, 각각 learning rate(step size)를 다르게 설정하고 이동하는 방식이다. (여기서 각각 이란 각 매개변수임을 말한다.)
epsilon 은 theta 를 갱신할 때 루트 안의 분모가 0이되는 것을 방지하기 위하여 아주 작은 값을 더한다는 의미이다.
현재까지 매개변수의 변화가 큰폭으로 변화한 경우 : Learning rate 를 decay 할 수 있겠다.
현재까지 매개변수의 변화가 작은폭으로 변화한 경우 : Learning rate 를 증가시켜야 한다.
** 혹시나 Loss function 의 Curve 가 아래로 오목한(Convex function) 함수가 아닐 수 있다. 위로 볼록한 경우 위의 것을 반대로 이해하길 바란다.
위의 학습에 대한 추정은 가장 먼저 변화가 큰 경우 대체로 그 값이 optimum 에 근접했다는 추정에 대한 설계이다.
* Word2Vec, Glove 와 같은 word representation 의 학습에서 단어의 등장 확률이 다르기 때문에 variable 의 사용 빈도차이가 발생한다. 때문에, AdaGrad 와 같이 각 매개변수의 수렴의 step size 를 다르게 해주는 방법이 효과적이다.
앞의 Word2Vec, Glove 와 같은 용어는 자연어 처리 (NLP)에서 등장하는 내용이므로 깊게 이해할 필요 없다.
수식으로 가자. v 는 먼저 각 매개변수에 대한 처리라고 언급하였으니 그 차원은 number of parameter 의 차원이 될 것이다.
간단하게 학습할 파라미터의 차원과 같다고 생각하면 된다. 그리고 v_t 라고 지칭한다면 time step t 까지 각 변수가 이동한 gradient 의 sum of squares 를 저장하는 것이다.
쉬운 이해로는 현재의 v 는 이전의 v 에 gradient 를 component-wise 하게 제곱하여 더했다는 것이다.
component-wise 란 : 행렬간 곱을 각 성분끼리 하는 것이다. (1, 1)의 성분은 다른 행렬의 (1, 1)의 성분과 곱해야 한다는 것.
이후 파라미터를 update 할 때, v 의 갱신된 값에 root 를 취한 값에 반비례하도록 나누어 준다. 이것은 변화의 양이 많은 매개변수라면 v 의 값이 클 것이고, 따라서 나눠주는 값이 커지기 때문에 그만큼 적은 보폭으로 update 되는 것이다.
4. RMSProp
AdaGrad 의 단점인 v 가 gradient 의 제곱 값을 더하기에 발생하는 무한정 커지는 문제에 대한 가능성을 해결가능하게 만들고자 고안되었다. 이것은 v 를 갱신하는 방법을 달리하는 것인데. 이전까지의 v 에 대한 정보를 이용하여 update 하는 것이다.
위의 v 에 갱신 방법을 지수이동평균(Exponential Moving Average) 라고 한다.

첫번째 수식만을 간단히 보겠다.
k = 0.1 이라고 가저앟겠다 그러면 이전 EMA(t-1) 데이터의 값의 0.9 ~> 90% 를 담겠다는 것이고 새로운 것을 0.1 만큼 갖겠다는 말이 된다. 너무 심플하게 말하고 있는 것 같아 그렇지만 이해만 되면 충분하다.

자 이제 본론으로 돌아와 RMSProp 의 update 에 대하여 보자.
이전에 우리는 이 수식을 간단하게 요약하고 넘어갈 것 이다.
E[g^2]_t ==> 의 경우 간단하게 h 라고 생각하자
g(t)^2 ==> gradient 의 제곱이다. [gradient 란 dL/dtheta 즉 Loss function 을 매개변수에 대하여 미분한 값이다.]
그렇다면, 첫번째 줄의 수식은 h <- gamma * h + (1 - gamma) * gradient^2
이것은 우리는 앞서 EMA 에서 보았듯이 간단하게 이해가 가능하다 gamma 라는 하이퍼 파라미터를 0.9라고 설정한다면 이전 time step 의 h 에 대한 정보를 90% 만큼 넘겨받고 새로운 값을 10% 만큼 받아 합쳐서 넘겨 주겠다는 말이 된다.
그리고 이것을 learning rate 에 root 를 취한 후 나누어 파라미터 갱신에 사용한다. 이것은 이전 AdaGrad 에서 설명했으니 넘어가겠다.
5. Adam (RMSProp + Momentum 의 결합체?)
타이틀에서 이미 언급되었지만, Adam 은 RMSProp 와 Momentum 의 장점을 서로 결합한 것이다.
(1) Momentum 방식과 유사하게 지금까지 계산해온 gradient 의 지수평균을 저장한다.
(2) RMS Prop 와 유사하게 기울기의 제곱 값의 지수평균을 저장한다.
간단하다 앞의 1, 2의 방법 모두를 적용하여 파라미터를 갱신한다.

식의 순서대로 momentum 과 rmsprop 라고 생각하면 같을 것이다. 각 파라미터를 다음과 같이 갱신하고 결과적으로 파라미터의 갱신은 다음과 같다.
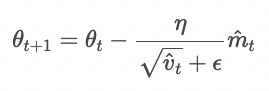
다만, 하나를 더 기억하고 넘어가자면 Adam 에서는 m과 v의 처음 값을 0으로 초기화하기에 학습 초반부의 0에 가깝게 bias 되어 있을거라는 판단을 할 수 있고 unbiased 되도록하는 작업을 수행한다.
m, v 를 각각 m_hat, v_hat 으로 추정하는 값으로 바꾸어 알고리즘을 수행한다.

** 주의할 것은 절대 beta1 과 beta2 를 같다고 생각하면 안된다. 서두에 말했던것 처럼 각각 다른 optimizer 의 연산자라고 생각해야한다.
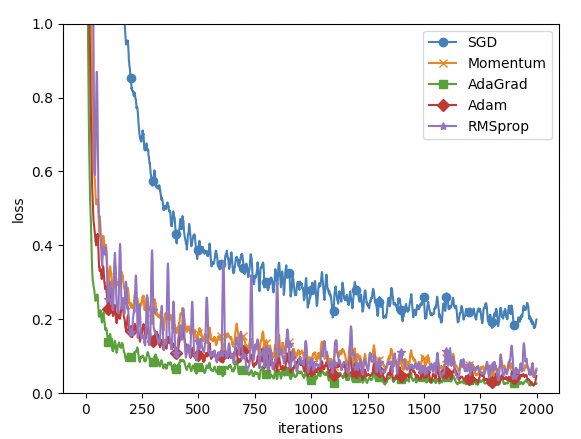
그렇다면, 전체적인 optimizer 에 대하여 동일한 네트워크를 바탕으로 어떻게 수렴하는지 확인하자.
데이터는 mnist 데이터 셋이다.