Extra) Hyperparameter Search
쉽지 않은 이해에 참고 자료 중 가장 효율적으로 정리할 수 있었던 본 포스팅의 내용은 https://www.youtube.com/watch?v=PTxqPfG_lXY 에 내용을 요약한 것이다.
나의 이해를 위한 것이기에 내용 정렬이 강의의 순서와 동일하다. 그러므로 좀 더 나은 이해를 위해 접속하여 확인하길 바란다.
Hyperparameter 란?
learning rate 와 같은 요소로서 학습에서 성능 향상에 중요한 도움을 줄 수 있는 세팅을 말한다.
가령 예를들어 learning rate 가 너무 작으면 학습의 속도가 너무 느려지게 되고 너무 크면 발산하여 수렴하지 않을 수 있다는 것이 이것의 중요성을 대변해주는 것이다.
Hyperparameter의 종류
Learning rate, Number of Layers, Batch size, Optimizer (SGD, Momentum, Adam), Activation function (Sigmoid, tanh, ReLU) 등이 있다.
Hyperparameter Search 의 방법들

두 방법은 오늘의 중점적인 내용이 아니기에 예를 들어, 간단히 설명하겠다
(1) Grid Search
Learning rate = [0.00001, 0.0001, 0.001, 0.01, 0.01]
Number of Layers = [10, 20, 30, 40, 50]
에 대하여 Hyperparameter 중 가장 최적의 값을 찾고자 한다면 learning rate 의 5가지와 # layers 의 종류 5가지에 대하여 번갈아 가며 모든 수행을 실시하는 것이다.
전체 25번의 학습을 Hyperparameter 를 수정하며 최적의 값을 찾도록 수행해야한다.
(2) Random Search
Grid Search 와 같이 격자 형태로 찾다보면 최적의 값을 놓칠 수 있다 위의 figure 를 확인하면 초록색 분포도에서 최적의 값을 갖는 점을 놓치고 있는데 이것은 규정된 값 안에서 찾으려면 아무래도 사람의 기준점에서 찾다보니 최적점을 놓치고 학습을 진행하는 경우가 생긴다.
하지만, Random Search 의 경우 특정 구간 내 값들을 모두 랜덤하게 찾아서 대입하며 최적점을 찾다보니 최적점에 도달할 가능성이 비교적 높다는 것이다.
* 이 역시 문제가 발생할 수 있다. 무엇이냐면 도대체 몇번을 학습해야 시행해야 최적점을 찾을 수 있냐라는 것이다.
가령 예로 상위 5% 성능을 발휘하기 위해서 몇번의 학습을 해야할지에 대한 추론으로 정리할 수 있다.
1 - (1 - 0.05) ^ n = 0.95 이 방정식을 풀어가면 대략 60회 정도의 학습 횟수가 필요하고 1% 의 경우 100번 정도에 달하는 학습이 필요하다. 이것은 결코 적은 것이 아니다.
우리의 새로운 문제는 과연 최소한의 학습 횟수로 최소한 어느정도의 성능을 보여줄 수 있는 최적의 점에 있는 Hyperparameter 를 찾아줄 수 있느냐라는 문제이다.
그렇기에 현재 가장 보편적으로 많이 사용되는 방법인 Bayesian Optimization 을 한번 볼 필요가 있다.
Hyperparameter Optimization 이란 정확하게 어떤일을 할까?
y = f(lambda) 라고 할 때, y 는 model performance 가 될 것이고, lambda 는 hyperparameter 가 될 것이다. 따라서 특정 lambda 를 사용하였을 때 가장 좋은 성능을 보이는 y 를 찾자는 것이다.
이것은 Black box Optimization 이라고 부를 수 있다.
왜냐하면 정답으로 알고 추정할만한 Objective function 이 없다는 것이다.
그렇기에 Gradient 를 구할 수 없다.
또한 직접 설정하고 계속해서 반복하며 다른 값들을 통하여 최적값을 찾아 가야하기에 값 비싼 비용을 지불해야한다.
Bayesian Optimization
1) 관측 데이터를 기반으로 f(x) 를 추정
- Bayes 정리를 활용 (f(x) 를 추정)
- Gaussian Process (f(x) 를 추정하기위해 사용)
2) 추정 모델을 기반으로 탐색할 파라미터를 선택
- 평균이 큰 것 (exploitation) (보편적으로 타당)
- 분산이 큰 것 (exploration) (불확실성을 먼저 제거하겠다라는 취지)
Gaussian Process 란?
Gaussian Distribution 은 random variable 에 대한 분포이고 평균과 분산으로 정의가 된다.
Gaussian Process 는 function 즉 y(model performance)이 Gaussian Distribution 즉 정규분포의 형태를 띌 것이라는 가정이다. 여기서 평균함수는 mu(x), 공분산함수(Covariance function) 은 k(x, x') 이 될 것이다.

1) 관측 데이터를 기반으로 f(x) 를 추정 : Gaussian Process
x : learning rate f(x) : accuracy
0.04 0.6
0.05(라고 한다면) 0.5 +/- 0.1 (대략 이러한 값을 갖지 않을까?) -> 평균이 크다 (exploitation)
0.06 0.3
0.08 0.4 +/- 0.3 -> 분산이 크다 (exploration)
0.09 0.5
2) 추정 모델을 기반으로 탐색할 파라미터를 선택 : acquisition function
말 그래도 추정 모델을 기반으로 탐색할 파라미터를 선택하는 함수를 acquisition function 라 한다.
acquisition function 함수의 기본 정책이 exploitation, exploration 혹은 둘을 절충하는 정책이 있다.
가령 평균이 큰 것에 대한 정책을 선택했다고 하면
x : learning rate f(x) : accuracy
0.04 0.6
0.05(를 실제로 사용하여 학습하면) 0.52 라는 Accuracy 를 얻게 된다.
0.06 0.3
0.09 0.5
정리해보면, 관측 데이터(기존에 주어진 데이터)를 기반으로 G.P 를 모델링 하고 acquisition function 이 최대값인 점을 찾아서 실제 값을 계산한다. 이때 얻은 데이터를 다시 관측 데이터에 추가하고 모델링을 계속해서 반복한다.
Acquisition function
acquisition function 은 최적화의 방향성을 제시한다.
이것은 실제 y 를 최대로 만들어 줄 수 있는 Hyperparameter 가 존재할 가능성이 높은 곳을 탐색하자는 내용과 일치하다.
- 평균이 최대
- 분산이 최대
- 평균과 분산은 trade off 관계이다.
Probability of Improvement (PI)
- 관측한 최댓값보다 더 클 가능성이 있는 지점을 찾는 것.
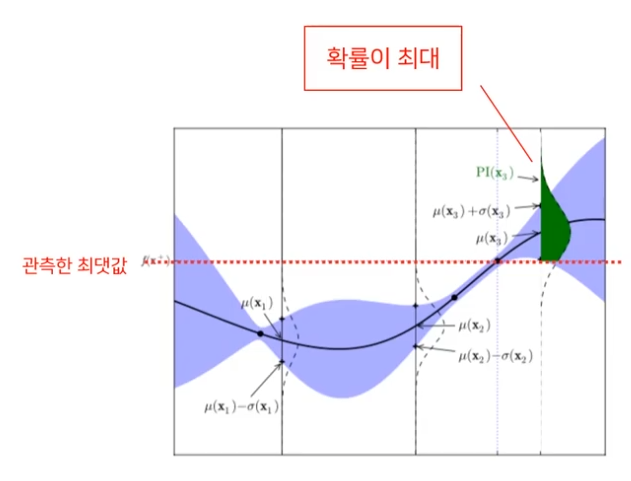
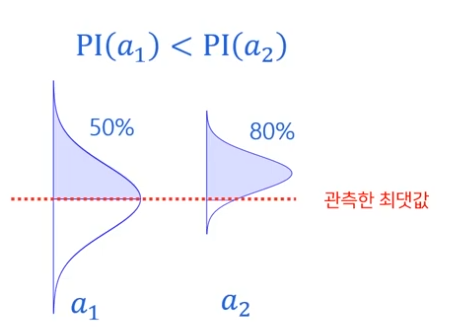
PI 방식에 대한 예를 들어 설명한 부분은
만약 복권의 당첨금이 10만원인 당첨확률이 80% 인 것(a2)과 당첨금이 100만원인 당첨확률이 50%인 것(a1)의 기준에서 PI 기준은 a2를 선택한다는 것이다.
Expected Improvement (EI)
- 실제 최댓값에 가까운 지점
= 실제 최댓값은 위치를 알 수 없기 때문에 관측한 최댓값 위쪽 영역의 기댓값이 최대인점
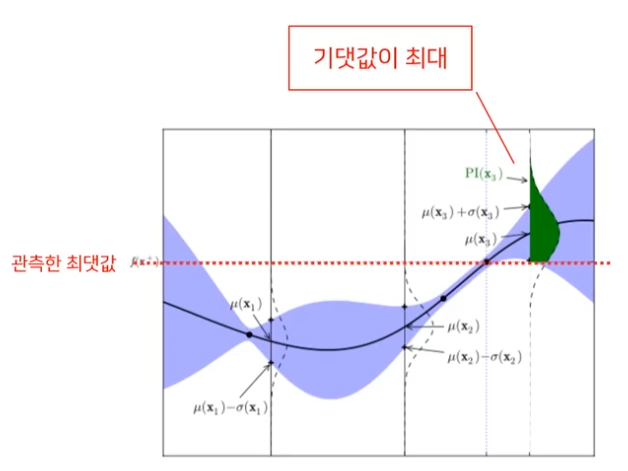
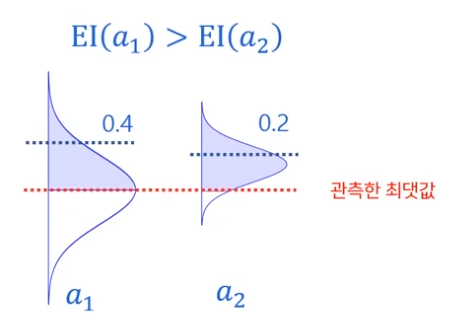
동일하게 EI 방식을 복권의 예로 보면
10만원이 80% 인 것은 기댓값이 10/8만원 정도 예상되고 100만원이 50% 인 것은 기댓값이 2만원 정도 될테니 기댓값이 높은 a1 를 선택하겠다는 것이다.
GP - Upper Confidence Bound (UCB)
- UCB 가 최대
argmax (mu(x) + k * sigma(x)) [sigma : standard deviation] (평균 + 표준편차)
가장 공격적인 방법으로 가장 클 가능성이 있는 지정을 먼저 선택하겠다 라는 의미를 담았다.
각 지점에서 평균과 표준편차를 어떻게 구할 것인가?
새로운 데이터 x* 에 대하여 f(x*) 의 평균과 분산을 추정

보통 이러한 covariance function 을 이용하여 위의 식과 같은 과정을 거치기도 하지만
scikit learn pakage 를 이용하면 더욱 간단하게 사용할 수 있다.
from sklearn.gaussian_process import GaussianProcessRegressor
gp = GaussianProcessRegressor()
gp.fit(data)
mean, std = gp.predict(data_new)
또한 이전의 Bayesian Optimization 을 Random Search 와 비교해보면
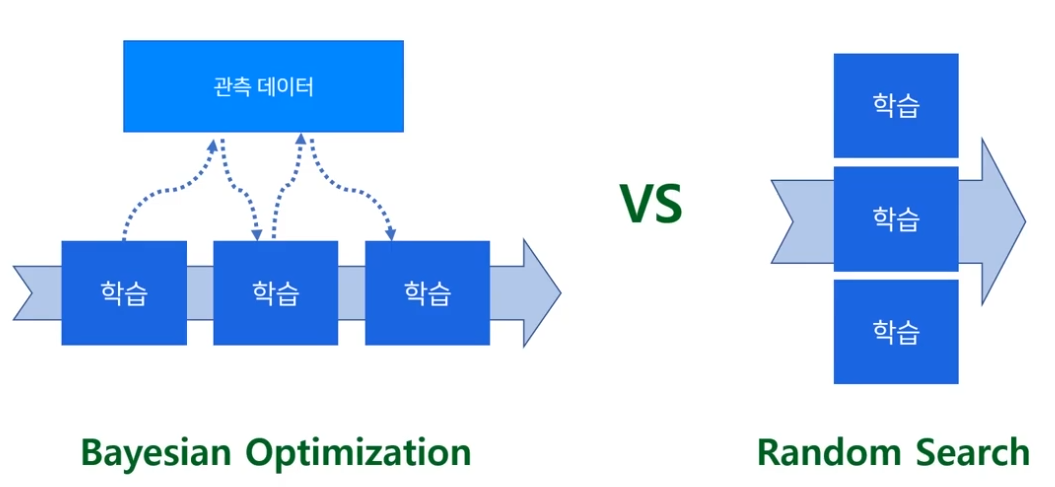
Bayesian Optim 은 Sequential data 의 방법이랑 유사하게 학습이 끝나면 그 데이터에 추가된 데이터로 다시 학습을 하기 때문에 Random Search 가 좀 더 빠르다는 것...
그렇기에 Parallel 한 방식을 사용하는데
Acquision function : Thompson Sampling
- 사후 분포를 기반으로 샘플링 하는 기법
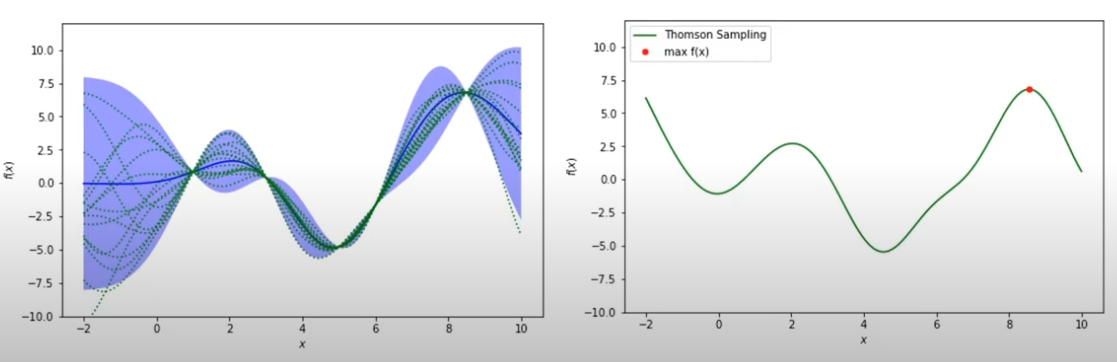
왼쪽에서 하나의 학습된 모델을 이용하여 굉장히 많은 샘플을 얻을 수 있고 그중 최적의 값(최댓값)을 사용하는 것이다.