오차역전파법이란 ?
- 가중치 매개변수의 기울기를 효율적으로 계산하는 방법이다.
이해하는 방법에는 크게 두 가지로 나눌 수 있다.
(1) 수식을 통한 이해
(2) 계산 그래프(Computation graph)로써의 이해
-목차-
(1) 계산 그래프
(2) 연쇄법칙
(3) 역전파
(4) 단순한 계층 구현
(5) 활성화 함수 계층 구현
(6) Affine / Softmax 계층 구현
(7) 오차역전파법 구현
1. 계산 그래프
계산 그래프는 계산 과정을 그래프로 나타낸 것이다. 전체적인 표현으로는 복수의 노드(node)와 에지(edge)로 표현하게 된다.
계산 그래프의 특징은 '국소적 계산'을 전파함으로써 최종 결과를 얻는다는 점에 있다.
계산그래프의 이점은?
가장 첫번째 이점은 앞서 언급된 국소적 계산이다. 전체가 아무리 복잡해도 각 노드에서는 단순한 계산에 집중하여 문제를 단순화 할 수 있다. 또 다른 이점으로는 계산그래프는 중간 계산 결과를 모두 보관할 수 있다는 점이다.
이것이 이점인 이유는 이후 언급될 역전파를 통해 '미분'을 효율적으로 계산할 수 있는 점이다.

2. 연쇄법칙 ~ 3. 역전파(Backpropagation)
계산 그래프의 figure 를 확인하면 순전파(forward propagation)는 계산 결과를 왼쪽에서 오른쪽으로 전달하였다. 이 순서는 앞서 여러번 동일하게 이어진 방식이니 자연스럽다. 하지만 역전파는 '국소적인 미분'을 순방향과는 반대인 오른쪽에서 왼쪽으로 전달한다. 또한 이 '국소적 미분'을 전달하는 원리는 연쇄법칙에 따른 것이다.

z 라는 연산이 앞선 x 와 y의 편미분으로 해석해보면 dL/dx 는 x의 일정량의 변화가 L의 변화에 얼마나 영향력을 행사하였는지에 대한 값이 될 것이고 y의 경우도 마찬가지이다. 하지만 우리는 이렇게 역전파학습을 진행하기에 앞서 dL/dx 즉 우리가 구하고자 하는 Loss function 에 x의 변화량이 얼마나 영향력을 갖는지에 대한 해석을 직접적으로 할 수 없다. 위의 figure 를 살펴보았다면 눈치 챘겠지만,
dL/dx = dL/dz * dz/dx 와 같이 이전 연산인 z에 대한 연산을 함께 고려해야한다. 결과적으로 이와 같이 역전파 학습은 이전 레이어의 결과에 대하여 차곡차곡 연산을 쌓아가는 과정이 될 것이다. 그러므로 연쇄법칙은 필수불가결하다.
4. 단순한 계층 구현
역전파를 위한 연산은 크게 두 가지 정도가 필요로 하다.
(1) 덧셈 노드 역전파
- 덧셈 노드 역전파는 입력 신호를 다음 노드로 출력할 뿐이다.
- 위의 figure 를 예로들면 z = x + y 와 같이 다음 노드로 입력이 넘어가고 결과적으로 Loss function 인 L 로 연산이 기록된다. 역전파를 이용하게 되면 결과적으로 x에 대한 연산을 구하려고 돌아가보면 dL / dz = dL / dz * dz / dx 와 같이 되고 dz / dx 가 1이기 때문에 특별한 연산없이 그저 신호를 넘겨주는 형태가 된다.
(2) 곱셈 노드 역전파
- 위에서 기록된 덧셈의 역전파에서는 상류의 값을 그대로 흘려보내서 순방향 입력 신호의 값이 필요하지 않았다. 하지만 곱셈의 역전파는 순방향 입력 신호의 값이 필요로 하게된다. 그래서 곱셈 노드를 구현할 때는 순전파의 입력 신호를 변수에 저장해두게 된다.
- z = x * y 라면 앞선 연산과 동일하게 진행하게된다면 dL / dz = dL / dz * dz / dx = dL / dz * y 가 되며 결과적으로 반대편의 문자가 기록에 곱해지는 구조로 연산이 이루어진다.

5. 활성화 함수 계층 구현
계산 그래프를 신경망에 적용할 때면 신경망을 구성하는 층을 각각 클래스 하나로 구현하며 backward term 을 추가해주게 된다.

간단하게, ReLU 와 Sigmoid function 에 대한 클래스 구현을 확인할 수 있다.
자세하게 각 함수의 derivative 에 대한 논의를 해보자.
(1) ReLU function
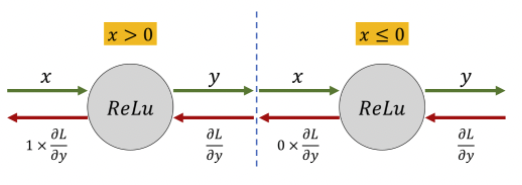
x > 0 이라면 x 를 출력 신호로 내어줄 것이고, x =< 0 이면 x = 0 으로 출력 신호를 내어주지 않는 것이 ReLU function 의 특징이었다.
미분을 해보면 x > 0 --> 1, x =< 0 --> x = 0 으로 생각할 수 있어 그리 큰 고민이 필요하지 않다.
(2) Sigmoid function
y = 1 / (1 + exp(-x)) 와 같이 구현된다.

이 블로그의 저자 분께서 올려주신 자료는 굉장히 도움을 많이 줄 수 있고 간결하게 이해할 수 있을 것 같았다.
결과적으로 해당 절차를 따라가 보면 d sigmoid(x) / dx = sigmoid(x) (1 - sigmoid(x)) 가 된다.
6. Affine / Softmax 계층 구현
(1) Affine 계층의 정의로 서술을 시작하려 한다.
- 신경망의 순전파 때 수행하는 행력의 곱을 기하학에서는 어파이 변환 (affine transformation) 이라고 한다. 그래서 이러한 변환 처리를 Affine 계층이라는 이름으로 구현한다.

Affine 계층의 구현은 forward 에서는 익숙하다 싶이 단순 Linear regression 과 동일한 연산이다. 다만 matrix form 으로 연산이 됨을 기억해야 한다.
backward 또한 앞선 곱셈과 덧셈 계층의 역전파와 동일하게 연산된다.
(2) Softmax with Loss 계층
자세히 다루지는 않겠지만, 꼭 언급하고 싶은 것은 소프트맥스 함수의 손실함수로 교차 엔트로피 오차를 사용하니 역전파가 (y1-t1, y2-t2, ... , yn-tn) 과 같이 깔끔하게 떨어지는데 이런 깔끔함은 우연이 아니라 교차 엔트로피 오차 즉 cross entropy error 라는 함수가 그렇게 설계되었기 때문이다. 또 회귀의 출력층에서 사용되는 항등함수 identity function 의 손실 함수로 sum of squared error 를 사용하는 이유도 이와 같다.

backward 파트에서 전파하는 값을 배치의 수로 나눠서 데이터 1개당 오차를 앞 계층으로 전파하는 점을 주의해서 알아두길 권하고 있다.
7. 오차역전파법 구현
이전 chapter4의 신경망 학습의 전체 구현과 동일한데.
(1) 미니배치
(2) 기울기 - backpropagation 가 동작하는 단계
(3) 매개변수 갱신 - gradient descent 가 동작하는 단계
(4) 반복
앞선 두 코드 구현을 확인하길 바란다. 비록 두 개의 층 뿐이지만, 전체적인 관계의 이해가 될 수 있는 좋은 코드라고 생각한다.
다만 GPU 를 사용할 수 없기 때문에 아쉽지만 시간은 조금 걸리는 것 같다.
데이터는 숫자를 손글씨로 표기한 mnist dataset 을 사용하였다.
0.9796833333333334 0.9699
[Finished in 11011.614s]'DeepLearningFromScratch' 카테고리의 다른 글
| 6.3 배치 정규화 (Batch Normalization) (0) | 2022.01.12 |
|---|---|
| 6.2 가중치의 초기값 (0) | 2022.01.12 |
| 6-1. 매개변수 갱신 (Optimizer and Optimization problem) (0) | 2022.01.12 |
| 4. 신경망 학습 (0) | 2022.01.11 |
| 3. 신경망 (Neural Network) (0) | 2022.01.10 |



